TRIÁNGULOS

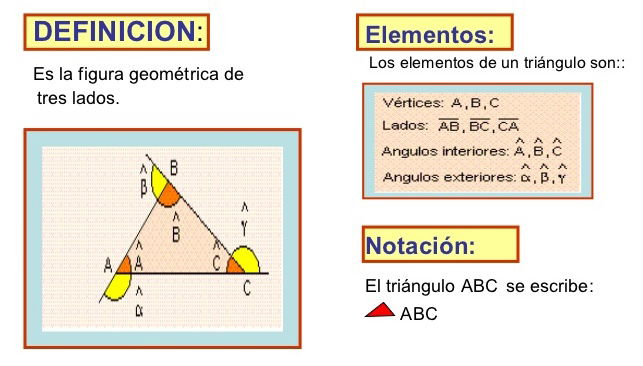
A, B Y C son tres puntos no colineales entonces la unión de los segmentos de AB,BC,AC, se denomina TRIANGULO y se denota ABC

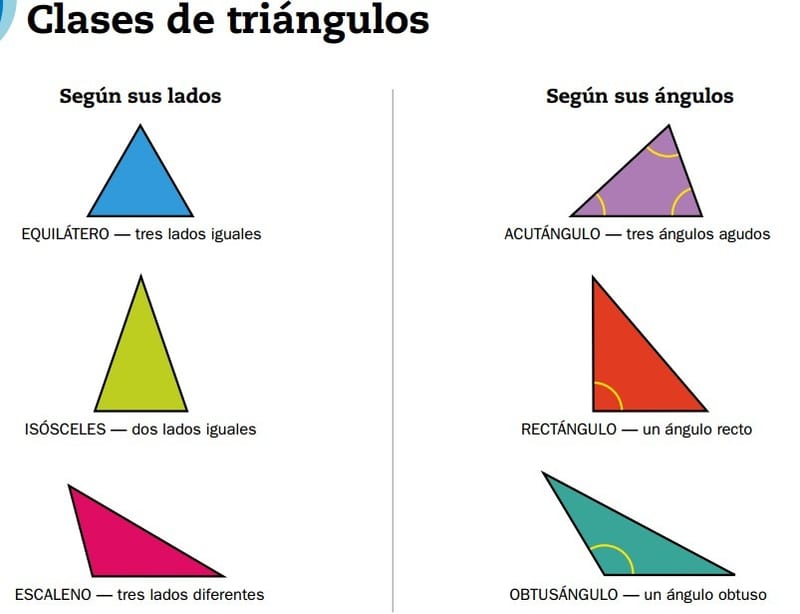
Existen diferentes tipos de triángulos según la longitud de sus lados Y según la medida de sus ángulos.

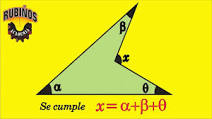
El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.

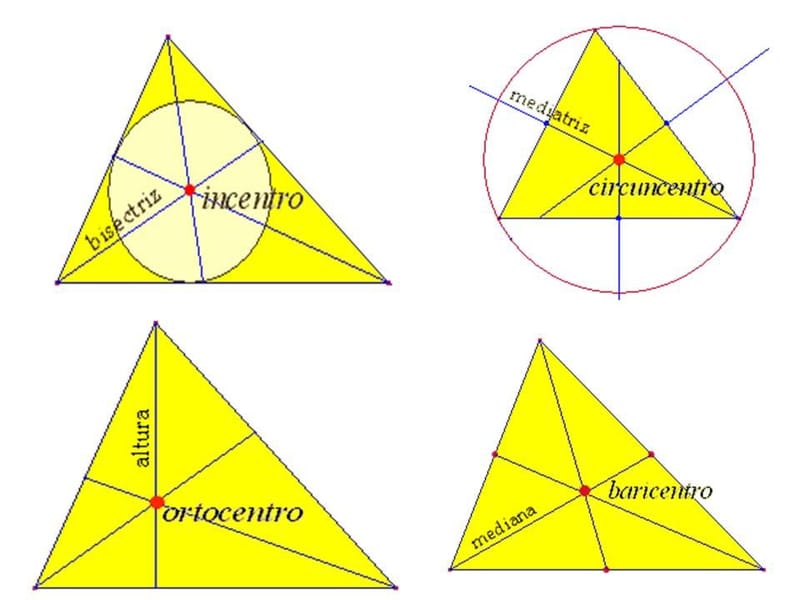
En un triángulo se trazan cuatro tipos de líneas notables. Las alturas, las medianas, las mediatrices y las bisectrices. Las intersección entre ellas generan los puntos notables ortocentro, baricentro, circuncentro e incentro respectivamente. En la figura se representan las alturas, las medianas y las mediatrices, así como sus respectivos puntos notables ortocentro, baricentro y circuncentro.

Teorema de Thales: Si dos rectas cualesquiera son cortadas por rectas paralelas, los segmentos que determina en una de las rectas son proporcionales a los segmentos correspondientes de la otra

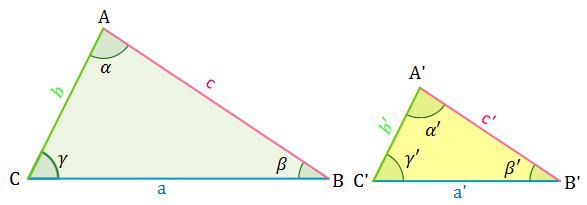
Los triángulos son semejantes cuando tienen sus ángulos iguales (o congruentes) y sus lados correspondientes (u homólogos) son proporcionales. Aquí tenemos un caso, donde se ven los elementos homólogos (ángulos y lados) con la igualdad o congruencia de sus ángulos y la proporcionalidad de los lados:

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Es la proposición más conocida entre las que tienen nombre propio en la matemática.